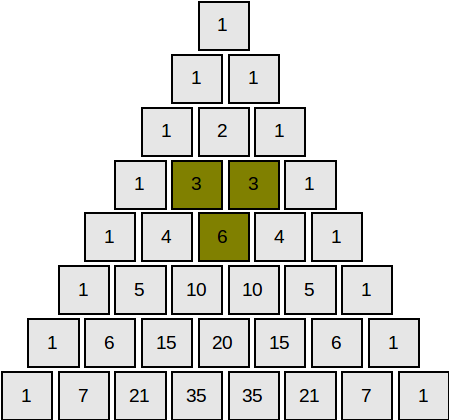
Triunghiul lui Pascal

Triunghiul lui Pascal este un tablou triunghiular cu numere naturale, în care fiecare element aflat pe laturile triunghiului are valoarea 1, iar celelalte elemente sunt egale cu suma celor două elemente vecine, situate pe linia de deasupra.

Forma matriceală

El poate fii rearanjat pentru stocarea în matrice astfel:

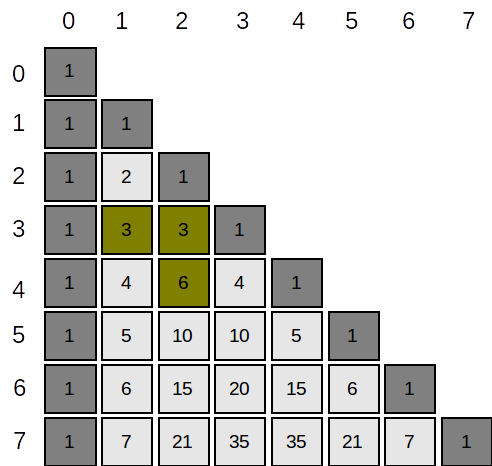
În forma matriceală el poate fii calculat ca: $M_{i,j}=\{\begin{array}{ll}1& \text{daca˘ }i=j\text{ sau }j=0,\\ M_{i-1,j-1}+M_{i-1,j}& \text{altfel}\end{array}$ De fapt, aceasta este relația din cazul combinărilor: $C_n^k=\{\begin{array}{ll}1& \text{daca˘ }n=k\text{ sau }k=0,\\ C_{n-1}^{k-1}+C_{n-1}^k& \text{altfel}\end{array}$ Sau tradus pentru matricea noastră folosind i și j: $C_i^j=\{\begin{array}{ll}1& \text{daca˘ }i=j\text{ sau }j=0,\\ C_{i-1}^{j-1}+C_{i-1}^j& \text{altfel}\end{array}$

• Elementele de pe linia n sunt coeficienți binomiali ai binomului lui Newton
• Suma elementelor de pe linia n este egală cu $2^n$
• Dacă considerăm matricea noastră ma fiind tp[m][m], $C_n^k$ va fii stocat în tp[n][k]

Generarea combinărilor folosind triunghiul lui Pascal

Evident pentru a genera combinările putem folosi metoda recursivă și putem aplica memoizarea pentru a o face mai eficientă. Totuși pentru a aplica programarea dinamică, vom folosi forma matriceală a triunghiului lui Pascal.

Cod

Varianta cu toată matricea

Pentru a calcula $C_n^k$ folosind Triunghiul lui Pascal urmăm pașii:

• Populăm prima coloană și diagonala principală cu valoarea 1
• Parcurgem începând cu i=2 (primele 2 rânduri sunt deja complete) și j=1 (prima coloană este completă) matricea.
• Parcurgem rândul cât timp j<i (înainte de diagonala principală, care este deja umplută)
• Ne oprim când i>n (trecem rândul pe care se află $C_n^k$)
  • Pe poziția tp[i][j] punem suma dintre valoarea direct de deasupra tp[i-1][j], și cea din stânga celei de sus tp[i-1][j-1] (tp[i][j] = tp[i-1][j-1] + tp[i-1][j]) În această rezolvare stocăm foarte multe date care nu sunt necesare, deși nu folosim decât linia anterioară, avem o complexitate de spațiu $O(n^2)$

#include <iostream>
using namespace std;
int tp[10][10];
int pascal(int n, int k){
    for(int i = 0; i <= n; ++i){
        tp[i][0] = tp[i][i] = 1;
    }
    for(int i = 2; i <= n; ++i){
        for(int j = 1; j < i; ++j){
            tp[i][j] = tp[i-1][j-1] + tp[i-1][j];
        }
    }
    return tp[n][k];
}
int main(){
    int n, k;
    cin >> n >> k;
    cout << pascal(n, k);
}

Varianta cu un singur vector

Totuși putem observa că în calcularea unui element folosim doar rândul anterior, nu și celelalte. Deci putem face soluția mai eficientă privind spațiul folosind un singur vector peste care scriem de mai multe ori. Trebuie să ținem cont de elementele folosite în calcul deoarece în calculul lui $C_n^k$ folosim $C_{n-1}^k$ și $C_{n-1}^{k-1}$, dar $C_{n-1}^{k-1}$ ar fii modificat în $C_n^{k-1}$ dacă am face generarea de la stânga la dreapta. Așa că vom genera combinările de la dreapta la stângă, păstrând astfel valorile de care avem nevoie (cea curentă și cea de la stânga) intacte cât timp avem nevoie de ele. Folosind doar un vector, complexitatea de spațiu ajunge la doar $O(n)$. La aceasta variantă nu mai există îmbunătățiri posibile.

Varianta iterativă

În această variantă la orice moment dat $C_n^k=C_{\text{level}}^{i-1}$ Deci, în level știm rândul pe care ne aflăm din forma matriceală a triunghiul lui Pascal, iar în i știm coloana c[level+1] este întotdeauna 1 pentru că indexarea începe de la 1

#include <iostream>
using namespace std;
void pascal(int niv, int c[]){
    int level = 1;
    c[1] = c[2] = 1;
    while(level < niv){
        level++;
        c[level + 1] = 1;
        for(int i = level; i >= 2; i--)
            c[i] += c[i-1];
    }
}
int main(){
    int c[1001], n, k;
    cin >> n >> k;
    pascal(n, c);
    cout << c[k];
    return 0;
}

Varianta recursivă

În această variantă la orice moment dat $C_n^k=C_{\text{niv}}^{i-1}$ Deci, în niv știm rândul pe care ne aflăm din forma matriceală a triunghiul lui Pascal, iar în i știm coloana c[niv+1] este întotdeauna 1 pentru că indexarea începe de la 1. Înainte de generarea liniei curente, apelăm pascal(niv-1, a) pentru a genera linia anterioară. Acest proces se oprește când niv==1, adică linia pe care sunt stocate $C_1^0$ și $C_1^1$

#include <iostream>
using namespace std;
void pascal(int niv, int a[]){
    if(niv == 1){
        a[1] = a[2] = 1;
        return;
    }
    pascal(niv - 1, a);
    for(int i = niv; i >= 2; i--)
        a[i] += a[i-1];
    a[niv + 1] = 1;
}
int main(){
    int a[1001], n, k;
    cin >> n >> k;
    pascal(n, a);
    cout << a[k];
    return 0;
}

Varianta aceasta s-a dat și în 2019 la admiterea de la UBB: Generarea Triunghiul lui Pascal fără structuri de date bidimensionale