Grafuri orientate

Terminologie

Definiție

Graf orientat = un graf $G=(V,E)$ în care relația binară nu este simetrică: $\forall (v,w)\in E,\nrightarrow \exists (w,v)\in E$

Vârf

Vârf = element al mulțimii $V$, unde $G=(V,U)$ este un graf orientat

Vârf izolat

Un vârf este izolat dacă are suma gradelor 0 Definiție alternativă: un vârf cu gradul interior 0 și gradul exterior 0

Vârf terminal

Un vârf este terminal dacă are gradul interior 1 și gradul exterior 0, practic dacă poți intra și nu mai poți ieși.

Arc

Arc = element al mulțimii $E$, ce descrie o relație existentă între 2 vârfuri din $V$, unde $G=(V,E)$ este un graf orientat

Extremitățile unui arc

Pentru arcul $(v,w)$ se numesc extremități ale sale nodurile $v$ și $w$

• $v$ se numește extremitate (vârf) inițială, iar $w$ extremitate (vârf) finală
• $v$ este predecesorul lui $w$, iar $w$ este succesorul lui $v$ Arcele sunt parcurse numai în direcția dată de relația $\text{predecesor}\to \text{succesor}$.

Adiacență

Vârful $w$ este adiacent cu vârful $v$ dacă perechea $(v,w)\in E$, deci $w$ este adiacent cu $v$ doar dacă este succesorul acestuia.

Această definiție este controversată deoarece pe pbinfo se definesc 2 noduri ca fiind adiacente dacă există un arc în orice sens între ele.

• ⏫ de clarificat definiția adiacenței in graful orientat

Incidență

Un arc este incident cu un nod dacă îl are pe acesta ca extremitate. Arcul $(v,w)$ este incident cu $v$ respectiv $w$. În cazul grafurilor orientate apar relațiile de incidență spre interior respectiv exterior.

Incidența spre interior

Un arc este incident spre interior cu un vârf dacă îl are pe acesta ca vârf terminal. Practic un arc este incident spre interior dacă acesta “intră” într-un vârf. Arcul $(v,w)$ este incident spre interior cu vârful $w$.

Incidența spre exterior

Un arc este incident spre exterior cu un vârf dacă îl are pe acesta ca vârf inițial. Practic un arc este incident spre interior dacă acesta “pleacă” sau “iese” dintr-un vârf. Arcul $(v,w)$ este incident spre exterior cu vârful $v$.

Grad

Grad interior

În cazul unui graf orientat fiecare vârf $v$ are are asociat un număr numit grad interior care este egal cu numărul de arce care îl au pe $v$ ca vârf terminal (numărul de arce incidente spre interior), sau numărul de noduri care îl au pe $v$ ca succesor, sau numărul de predecesori ai lui $v$.

Grad exterior

În cazul unui graf orientat fiecare vârf $v$ are are asociat un număr numit grad exterior care este egal cu numărul de arce care îl au pe $v$ ca vârf inițial (numărul de arce incidente spre interior), sau numărul de noduri care îl au pe $v$ ca predecesor, sau numărul de succesori ai lui $v$.

Teoreme și proprietăți

• Într-un graf orientat, suma gradelor exterioare a tuturor vârfurilor este egală cu suma gradelor interioare a tuturor vârfurilor și cu numărul de arce.
• Un vârf se numește izolat dacă gradul interior și gradul exterior sunt ambele egale cu 0.

Drum

Drumul este o secvență de vârfuri ale unui graf orientat $G=(V,E)$ legate fiecare de următorul printr-un arc. Trebuie să poată fii parcurs pe direcția de mers a arcului, în secvența $\text{predecesor}\to \text{succesor}$. $w_1,w_2,w_3,...,w_n$ cu proprietatea că $(w_i,w_{i+1})\in E,1\le i<n$ $(3,5,4)$ este un drum, dar $(1,6,2)$ nu este un drum Proprietățile drumurilor și tipurile lor sunt similare cu cele ale lanțurilor.

Lungimea unui drum

Lungimea unui drum este numărul de arce din care este format

Drum simplu

Drumul simplu este drumul care conține numai arce distincte

Drum compus

Drumul compus este drumul care nu este format numai din arce distincte. Practic, dacă un drum nu este simplu, este compus.

Drum elementar

Drumul elementar este drumul care are numai vârfuri distincte

Circuit

Circuitul este un drum în care primul vârf coincide cu ultimul.

Lungimea unui circuit

Lungimea unui circuit este egală cu numărul de arce.

Circuit simplu

Circuitul simplu este un circuit în care nu se repetă nici un arc.

Circuit compus

Circuitul compus este un circuit care nu este format numai din arce distincte. Practic dacă un ciclu nu este Circuit simplu, este compus.

Circuit elementar

Un circuit este elementar dacă este format doar din vârfuri distincte, excepție făcând primul și ultimul. Implicit asta înseamnă că nu se repetă nici un arc. Deci orice circuit elementar este implicit și simplu, dar nu și invers.

Bucla

Bucla este un circuit format dintr-un singur arc și implicit un singur nod. Aceasta este reprezentată în $E$ ca $(v,v)$.

Tare conexitate

Fie graful orientat $G=(V,E)$ Graful se numește tare conex dacă între oricare două vârfuri distincte există cel puțin un drum. Se numește componentă tare conexă un subgraf tare conex și maximal cu această calitate – dacă am mai adăuga un vârf, n-ar mai fi tare conex. Exemplu: 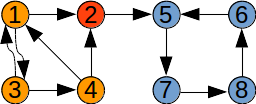Graful de mai sus nu este tare conex. El conține trei componente tare conexe formate din următoarele vârfuri:

• 1 3 4
• 2
• 5 6 7 8

Atenție: Un vârf al grafului face parte dintr-o singură componentă tare conexă. Dacă ar face parte din două componente tare conexe, ele s-ar “reuni” prin intermediul acelui vârf.

Acest articol conține mai multe detalii despre tare-conexitate (algoritmi de verificare a tare conexității, de determinare a componentelor tare-conexe, etc.).

Tipuri de grafuri orientate

Graf tare conex

Graful se numește tare conex dacă între oricare două vârfuri distincte există cel puțin un drum.

Graf complet

Graful $G$ se numește graf complet dacă oricare două vârfuri distincte ale sale sunt adiacente (vom folosi definiția de pe pbinfo)

• Numărul de grafuri orientate cu $n$ vârfuri este $3^{\frac{n(n-1)}{2}}$
• Nu putem știi numărul de arce într-un graf complet

Graf nul

$G=(V,\varnothing )$ Graful nul este graful în care nu există muchii, sau în care mulțimea muchiilor este vidă $E=\varnothing$. A nu fi confundat cu cu graful vid. Graful complementar al grafului nul este graful complet.

Graf turneu

Graful $G$ se numește graf turneu dacă oricare ar fi 2 vârfuri distincte, între ele există un singur arc: pentru vârfurile $i$ și $j$ există arcele $(i,j)$ sau $(j,i)$ dar nu ambele.

• Orice graf turneu este și complet (dar nu și invers)
• În orice graf turneu există un drum elementar care trece prin toate vârfurile grafului.
• Numărul de grafuri turneu cu $n$ vârfuri este $2^{\frac{n(n-1)}{2}}$

Graf orientat hamiltonian

• Drumul elementar care conține toate vârfurile se numește hamiltonian.
• Circuitul elementar care conține toate vârfurile se numește hamiltonian.
• Graful care conține un circuit hamiltonian se numește hamiltonian.

Condiție de suficiență

Dacă $G$ este un graf cu $n\ge 3$ vârfuri astfel încât gradul oricărui vârf verifică inegalitatea $gr(x)\ge \frac{n}{2}$ rezultă că $G$ este graf hamiltonian. Este foarte rar folosită, nu se întâmplă des ca un graf hamiltonian să îndeplinească această condiție (este suficientă, nu necesară)

Graf orientat eulerian

• Drumul simplu care conține toate arcele se numește eulerian.
• Circuitul simplu care conține toate arcele se numește eulerian.
• Graful care conține un circuit eulerian se numește eulerian.

Condiție necesară și suficientă

Un graf orientat este eulerian dacă și numai dacă:

• Este conex
• Oricare vârf are gradul interior egal cu gradul exterior

Reprezentarea grafurilor orientate

Matrice de adiacență

Fie $G=(V,E)$ un graf orientat cu $n$ vârfuri, în care nu există mai multe arce de la un nod la altul. Matricea de adiacență $A$ a grafului este o matrice cu $n$ linii și $n$ coloane și elemente din $\{0,1\}$, astfel: $A_{i,j}=\{\begin{array}{ll}1& \text{daca˘ }(i,j)\in E\\ 0& \text{daca˘ }(i,j)\notin E\end{array}$ Pentru graful de mai jos, matricea de adiacență este: $A=\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 1\\ 1& 0& 0& 1& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 1& 1& 0& 1& 0& 0\end{array}\right)$

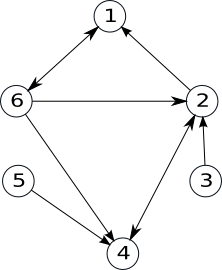
• are zerouri pe diagonala principală (dacă în graf nu avem bucle)
• nu trebuie să fie simetrică față de diagonala principală

Lista de arce

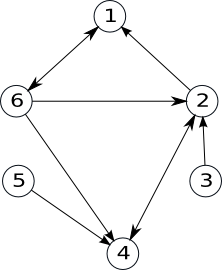
Lista de arce a unui graf orientat reprezintă o mulțime (familie, dacă arcele se pot repeta) ce conține toate arcele din graf. Pentru graful mai jos, lista de arce este: $E=\{(1,6),(2,1),(2,4),(3,2),(4,2),(5,4),(6,1),(6,4)\}$

Reprezentarea în memorie

Pentru reprezentarea în memorie putem folosi:

• un tablou unidimensional cu elemente de tip struct {int I,J;}
• două tablouri unidimensionale cu elemente de tip int
• o listă alocată dinamic
• etc.

Liste de adiacență (succesori)

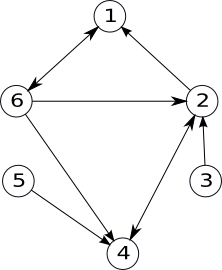
Pentru un graf orientat cu $G=(V,E)$ se va memora numărul de [[#Vârf|#vârfuri]] $n$ și apoi, pentru fiecare vârf $x$, lista succesorilor lui $x$, adică vârfurilor $y$ cu proprietatea că există arcul $(x,y)\in E$. Pentru graful de mai jos acestea sunt:

1: 6
2: 1 4
3: 2
4: 2
5: 4
6: 1 2 4

Reprezentarea în memorie

La reprezentarea în memorie trebui avut în vedere că dimensiunile listelor de succesori sunt variabile. De aceea, este ineficientă (dar posibilă folosind o matrice cu n linii și n coloane) utilizarea unor tablouri alocate static. Astfel, putem folosi:

• un șir de n tablouri unidimensionale alocate dinamic;
• un șir de n vectori din STL;
• un șir de n liste simplu (dublu) înlănțuite alocate dinamic.