Plata2

În problema #3169 - Plata2 de pe#pbinfo generăm o soluție pentru a plăti o sumă specificată cu un număr de bancnote specificate cu valori specificate, folosind minim o bancnotă din fiecare.

Cerința

Se consideră n tipuri de bancnote, cu valorile v[1] v[2] ... v[n], ordonate strict crescător. Pentru fiecare tip de bancnote se știe numărul de bancnote disponibile c[1] c[2] ... c[n]. Se cere să se determine o modalitate de a plăti integral o sumă dată S cu bancnotele disponibile, astfel încât să se folosească cel puțin o bancnotă de fiecare tip.

Explicație

Varianta naivă la acest exemplu ar fii să generăm toate combinațiile posibile de bancnote și să verificăm la final dacă care dintre ele este validă.

Varianta corectă

• Presupune din start că se folosește câte o bancnotă din fiecare și calculează suma rămasă, afișarea făcându-se la final cu +1 pentru a “pune” la loc bancnota care a fost scăzută din start.
• Ulterior folosim backtracking ca să generăm doar variante care sunt posibil corecte, adică scădem din suma rămasă doar până aceasta ajunge la 0, iar apoi ne oprim.
• Dacă nu am parcurs încă toate valorile de bancnote, trecem la următoarea bancnotă prin creșterea lui k care reprezintă “pasul” și generăm posibilitățile și acolo. Altfel, dacă suma rămasă a ajuns la 0 și noi am ajuns la ultima bancnotă, marcăm ok=1 și algoritmul nu mai continuă. Dacă niciunul dintre aceste cazuri nu este îndeplinit, funcția face ”backtrack”
• Adunăm la loc valoarea care s-a scăzut la începutul încercării acesteia, ca sumaramasa să fie pregătit pentru următoarea încercare.

Astfel, se reduce numărul de variante greșite, condiția de minim o bancnotă fiind îndeplinită de la început, singura situație în care o cale greșită este luată e dacă la final suma rămasă nu este divizibila de prin valoarea ultimei bancnote, caz în care funcția face ”backtrack” și încearcă să mărească nr de bancnote cu valoarea anterioară.

Soluția:

#include <iostream>
using namespace std;
int v[6], c[6], x[6], n, s;
bool ok=0;
void generare(int k, int  sumaramasa){
for (int i = 0; i <= c[k] && sumaramasa-i*v[k]>=0 && !ok; i++)
    {
        sumaramasa-=i*v[k];
        x[k]=i;
        if(k<n-1)
            generare(k+1, sumaramasa);
        else if(sumaramasa==0&&k==n-1)
            ok=1;
        sumaramasa+=i*v[k];
    }
}
int main(){
    cin >> n >> s;
    for (int i = 0; i < n; i++)
        cin >> v[i];
    for (int i = 0; i < n; i++){
        cin >> c[i];
        c[i]--;
        s-=v[i];
    }
    generare(0,s);
    for (int i = 0; i < n; i++)
        cout << x[i] +1 << " ";
}

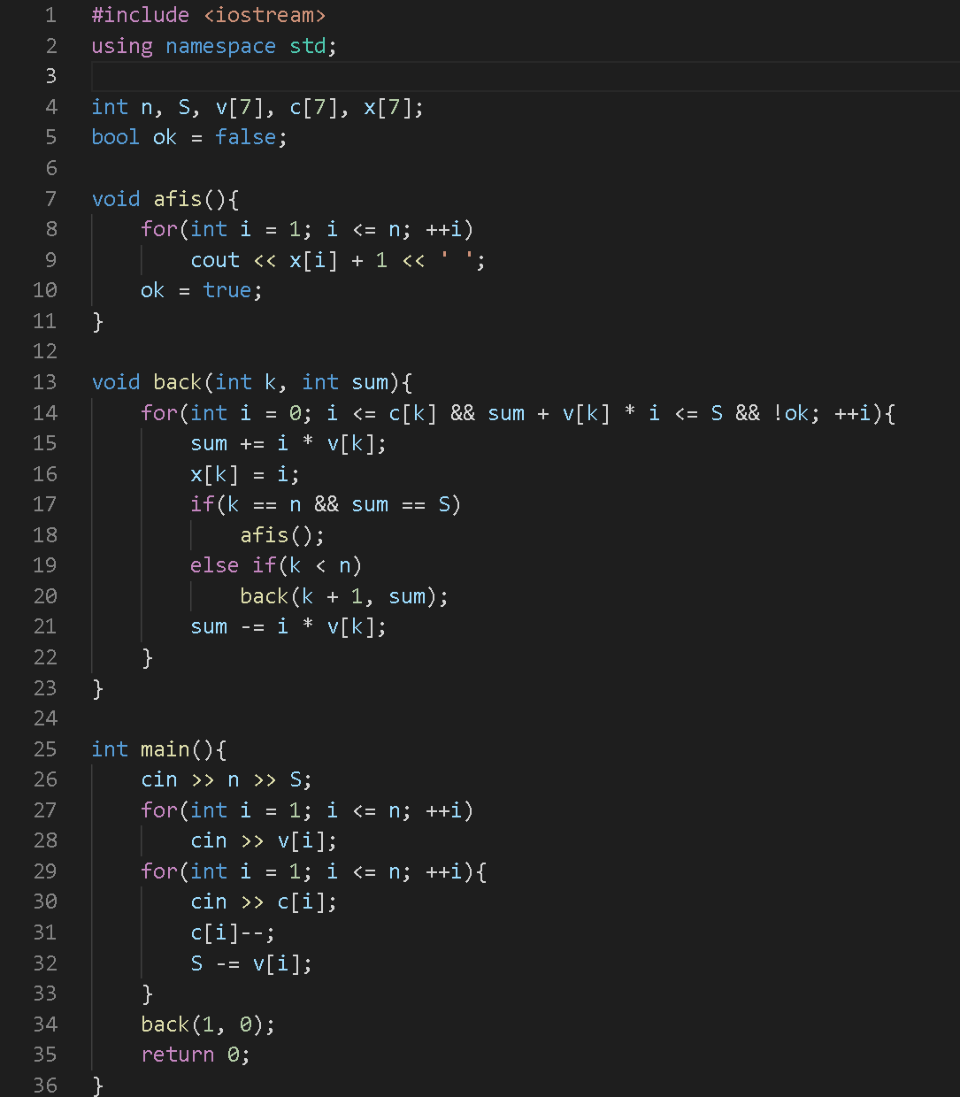
Varianta din curs:

• sum din argumentul funcției este suma acumulată până în acel moment, spre deosebire de varianta de mai sus care folosește sumaramasa .